|
|
|
 |
|
|
|
|
|
|
Ancient Navigators Could Have Measured Longitude!
by Rick Sanders
(Full text of article from Fall 2001 21st Century)
|

From America B.C.,© Barry Fell (New York: Simon & Schuster, 1976), p. 118
Drawing by Maui of his tanawa or calculator, found in the Caves of the Navigators, Sosorra, Irian Jaya (West New Guinea).
|
|
Around the year 232 B.C., Captain Rata and Navigator Maui set out with a flotilla of ships from Egypt in an attempt to circumnavigate the Earth.1 On the night of August 6-7, 2001, between the hours of 11 PM and 3 AM, this writer, and fellow amateur astronomer Bert Cooper, proved in principle that Captain Rata and Navigator Maui could have known and charted their location, by longitude, most of the time during that voyage.
The Maui expedition was under the guidance of Eratosthenes, the great scientist who was also the chief librarian of the library at Alexandria. Could this voyage have demonstrated Eratosthenes' theorem that the world was round, and measured approximately 24,500 miles in circumference? One of the navigational instruments which Maui had with him was a strange looking "calculator" that he called a tanawa; such an instrument was known, in 1492, as a torquetum.
Intrigued by a photograph of the cave drawing of that tanawa in Irian Jaya, western New Guinea, I speculated that Maui must have been looking at the ecliptic to measure "lunar distance," in order to find his longitude. Maui's tanawa was of such importance, that he drew it on the cave wall with the inscription, deciphered in the 1970s by epigrapher Barry Fell: "The Earth is tilted. Therefore, the signs of half of the ecliptic watch over the south, the other (half) rise in the ascendant. This is the calculator of Maui."
Eratosthenes had just measured the circumference of the Earth, and the circumference of a sphere is the same in all directions. We know that Maui was thinking about this, because his cave drawings also include a proof of Eratosthenes' experiment to measure the Earth's circumference.
To test the hypotheses, we built a wooden torquetum and used a simplified version of it to measure the change in angular distance between the Moon and the star Altair, in the constellation Aquila (the Eagle). This success proves official dogma wrong, and proves that, in principle, Navigator Maui, during his voyage could have used tables brought from Alexandria, drawn up by Eratosthenes or his collaborators, compared those lunar distances with the distances that he measured, and come up with a good estimate of his longitude.
It is important to note that we are not claiming here that we know everything about the torquetum. We simplified our device for the proof-of-principle experiment, but we will carry out and report on more experiments, using the full instrument.
|

The author, using an equatorial sundial to establish a north-south line.
|
|
The torquetum's value, as an analogue calculator, must have been immense, because, once a planet or the Moon are not on the meridian, all "straight lines" become curves—so that calculations are difficult, even with a modern calculator. However, the 23.5-degree plane on the torquetum allows one to directly read the longitude and latitude of a planet or the Moon, relative to the ecliptic, without calculation. These data would be invaluable for predicting eclipses and occultations of various stars or planets by the Moon.
The Inspiration for the Experiment
This was intriguing! What was this "tanawa" for? Why the 23.5-degree plane, characteristic of the torquetum? It could only mean that Maui was looking at the ecliptic, the Moon, and the planets, the "wandering stars."
Of the two torquetums surviving in the world, one belonged to Nicholas of Cusa, and the other to Regiomontanus, both of whom were involved in calendar reform, including setting the date of Easter, which, along with some other religious festivals, is dated by the interaction of the lunar and solar calendars.
But what could Maui have been doing? Trying to determine longitude? The very thought was heretical. To take things out of the realm of speculation, the only solution was to build a torquetum, and see if longitude could be determined by using sightings of the Moon, with simple backyard equipment; if this succeeded, then Navigator Maui could have also succeeded.
|
|
|
|
|
|
 |
|
|
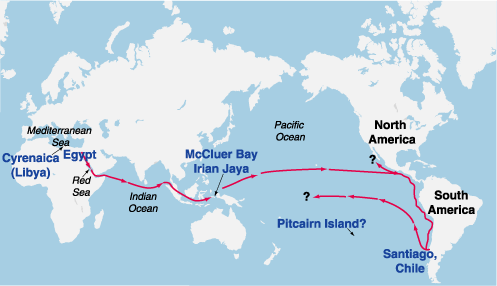
Figure 1
PROBABLE ROUTE OF THE EGYPTIAN VOYAGE IN 232 B.C.
Deciphered rock and cave inscriptions from the Pacific islands, western New Guinea, and Santiago, Chile, tell of an Egyptian flotilla that set sail around 232 B.C., during the reign of Ptolemy III, on a mission to circumnavigate the globe. The six ships sailed under the direction of Captain Rata and Navigator Maui, a friend of the astronomer Eratosthenes (ca. 275-194 B.C.), who headed the famous library at Alexandria. Maui's inscriptions, as deciphered in the 1970s by epigrapher Barry Fell, indicated that this was a proof-of-principle voyage, to demonstrate Eratosthenes' theorem that the world was round, and approximately 24,500 miles in circumference.
|
|
|
|
|
|
|
Finding Longitude
You cannot tell longitude from the stars alone, because their daily motion is purely apparent, caused by the rotation of the Earth. At 8 PM (solar apparent time), any star, seen from anywhere, whether Ferrara, Paris, or Cairo, will have the same azimuth as it does in Washington, D.C., Chicago, Sioux Falls, S.D., Seattle, or anywhere else. The Moon shares in this apparent motion to the west, but it also has its own independent, real motion.
Look at what Amerigo Vespucci, himself at the frontiers of post-Dark-Ages navigational astronomy, said of this in 1502, in Letter IV:
". . . I maintain that I learned [my longitude] . . . by the eclipses and conjunctions of the Moon with the planets; and I have lost many nights of sleep in reconciling my calculations with the precepts of those sages who have devised the manuals and written of the movements, conjunctions, aspects, and eclipses of the two luminaries and of the wandering stars, such as the wise King Don Alfonso in his Tables, Johannes Regiomontanus in his Almanac, and Blanchinus, and the Rabbi Zacuto in his almanac, which is perpetual; and these were composed in different meridians: King Don Alfonso's book in the meridian of Toledo, and Johannes Regiomontanus's in that of Ferrara, and the other two in that of Salamanca."2 The best "clock" to use for reference, is the stars. In the roughly 27.3 solar days of a lunar orbit, the Moon moves a full 360 degrees around the sky, returning to its old position among the stars. This is 13 degrees per day, or just over 0.5 degree per hour. So, while the rotation of the Earth causes the stars and the Moon to appear to move from east to west across the night sky, the Moon, because of its own orbit around the Earth, fights back against this apparent motion, and seems to move eastward (or retrograde) by about 0.5 degree per hour. In other words, the Moon "moves" west only 11.5 degrees per hour.
|
|
|
|
|
|
|
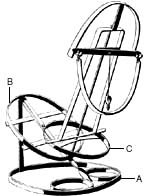 A brass model of Maui's tanawa, constructed by Dr. Sentiel Rommel. The base (A) in the plane of the observer's horizon, is oriented so that the axis of symmetry is parallel to the meridian. (B) is the equatorial plane. (C) is the ecliptic plane (viewed from one side in Maui's drawing, hence appearing as a line). A brass model of Maui's tanawa, constructed by Dr. Sentiel Rommel. The base (A) in the plane of the observer's horizon, is oriented so that the axis of symmetry is parallel to the meridian. (B) is the equatorial plane. (C) is the ecliptic plane (viewed from one side in Maui's drawing, hence appearing as a line).
Drawing by Matt Makowski in The Epigraphic Society Occasional Publications, Vol. 32, No. 29, Feb. 1975
|
|
|
|
|
|
|
Thus, if a known star is in a given position on the celestial sphere (measured by azimuth and right ascension), a table could be drawn up at a given location for each night, showing how distant the Moon appears to be from that star.
For example: If a ship sailed west out of a port, and its new longitude were now 15 degrees west (one hour) of that port, and those on the ship could see the Moon and the reference star, the Moon would appear to be 0.5 degree east of where the table would show it to be for the port of departure. There is nothing here that navigator Maui in 232 B.C. could not have known. The only question would be whether his instruments could measure an angular difference on the order of 0.5 degree.
Our Observations
Our observational experiment showed that a simplified torquetum could do it. In the time that Altair had moved 41.8 degrees west along the equatorial plane, the Moon had moved only 40.25 degrees, a difference of 1.55 degrees. Because the Moon should retrograde about 0.5 degree/hour, the calculated regression would equal 1.39 degrees. This error of less than 1/6th (or 0.166) of a degree is well within our instrument limitations, which can be read only to 0.25 of a degree.
Notes
1. For the story of the Rata-Maui Expedition, see "The Decipherment and Discovery of a Voyage to America in 232 B.C.," by Marjorie Mazel Hecht, 21st Century, Winter 1998-1999, p. 62; "Indian Inscriptions from the Cordilleras in Chile" found by Karl Stolp in 1885, 21st Century, Winter 1998-1999, p. 66; "On Eratosthenes, Maui's Voyage of Discovery, and Reviving the Principle of Discovery Today," by Lyndon H. LaRouche, Jr., 21st Century, Spring 1999, p. 24; "Eratosthenes' Instruments Guided Maui's 3rd Century B.C. Voyage," by Marjorie Mazel Hecht, 21st Century, Spring 1999, p. 74; and "Maui's Tanawa: A Torquetum of 232 B.C.," by Sentiel Rommel, Ph.D., 21st Century, Spring 1999, p. 75.
2. Cited in Letters From A New World, 1992. Ed. Luciano Formisano (New York: Marsilio Publishers), pp. 38-39.
|
|
|
|
|