|
|
|
 |
|
|
|
|
|
Was the Antikythera an Ancient Instrument for Longitude Determination?
by Richard Sanders
(Reprinted in full from 21st Century, Spring 2003)
|
BUY THIS ISSUE
U.S.
Foreign
For more on ancient navigation devices, see "Ancient Navigators Could Have Measured Longitude!" by Richard Sanders, and "Building and Using Maui's Tanawa," by Bertram Cooper.
|
|
In the wake of our work on the torquetum,1 there has been renewed interest in ancient, or not so ancent, astronomical instruments. Henry Aujard in France recently brought to our attention one of the most important archaeological finds of the 20th Century (or perhaps of modern times): a very intricate, bronze, geared instrument, known as an antikythera, which dates from around 80 B.C. Fragments of the instrument were found in a large shipwreck on the sea floor off the coast of Greece in 1900, by sponge fishers. (See Figure 1.) It is unlike anything else that has been passed down to us, in terms of the intricacy of its more than 30 gears. (We do have a geared astrolabe, but it is from about 1,000 years later!).
The antikythera was studied over the years, but the breakthrough came when Derek de Solla Price, a professor of the history of science at Yale University, was able to use gamma-radiography in 1972 to look at the fragments in intricate detail. He presented his analysis in a 1974 article published by the American Philosophical Society,2 whose study we have just begun. We are writing this communication to urge others to also study the 1974 work.
|
|
|
|
|
|
|
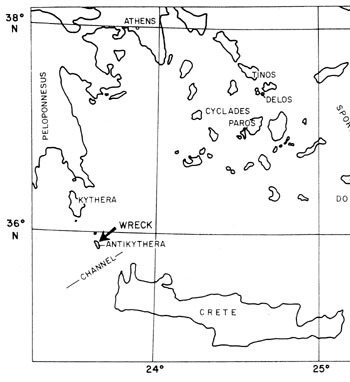 |
Figure 1
THE ISLAND OF ANTIKYTHERA
Location of the wreck, near an island between Kythera and Crete, from which the antikythera fragments were salvaged.
Source: Derek de Solla Price, "Gears from the Greeks," Transactions of the American Philosophical Society (New Series), Volume 64, Part 7, 1974, Figure 1.
|
|
|
|
|
|
|
De Solla Price must be commended for his scrupulous attempts to decipher the significance of the ratios of the gears, as involving the relative motions of the Sun and the Moon, including the Metonic cycle (in which 19 solar years correspond exactly with 235 lunations). But the outstanding question that, to our knowledge (and we hope to be wrong), no one has asked is: Why would anyone want to fool with the Moon? It is the same question which we confronted in our hypotheses about the torquetum.
So, let us exclude Moon worshippers and religious rituals as explanation. Otherwise, the Moon is useful for tidal information, and for telling fishermen when the fish are biting, but such information does not justify a "Mount Palomar" instrument such as the antikythera, which, after all, was being carried on a ship.
|
|
|
|
|
|
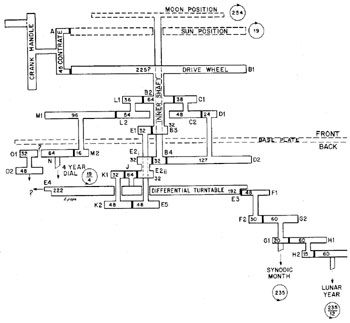 |
Figure 2
DIAGRAM OF THE ANTIKYTHERA GEARING SYSTEM
De Solla Price’s diagram of the antikythera’s complete gearing system.
Source: Derek de Solla Price, "Gears from the Greeks," 2ransactions of the American Philosophical Society (New Series), Volume 64, Part 7, 1974, Figure 33.
|
|
|
|
|
|
|
The only reasons for a sailor/navigator to mess with the Moon is to predict eclipses (for finding longitude), and to forecast lunar distances (to find longitude). As we pointed out in the article on the torquetum, if you are using the Moon to determine longitude, you must have with you a book of tables, in which the position of the Moon (for a point of reference), would be given relative to various stars, preferably over 19 years.
The advantage of a geared mechanism, which would have to be set, or be settable, for a given longitude (that is, reference place), would be that you could dispense with the tables. All you would have to do is crank the handle for the number of days since you left port, and that would give you the longitude of the Moon for that day, for your home base, or place of reference. Then, you could measure the Moon’s position relative to some appropriate bright star, and you would know your longitude.
We are putting out this communication to provoke discussion.
Notes
1. See Rick Sanders, "Ancient Navigators Could Have Measured Longitude!" and Bertram Cooper, "Building and Using Maui’s Tanawa, 21st Century, Fall 2001, pp. 58-65.
2. "Gears from the Greeks," Transactions of the American Philosophical Society (New Series), Volume 64, Part 7, 1974, pp. 1-70.
|
|
|
|
|
|
|
|
De Solla Price on ‘Gears from the Greeks’
Excerpted, with permission, from Derek de Solla Price, "Gears from the Greeks," Transactions of the American Philosophical Society (New Series), Volume 64, Part 7, 1974.
"It seems that the function of the turntable must be to take these two rates of revolution, one annual and the other approximately monthly, and compound them either as a sum or a difference. The two obvious and almost inescapable astronomical choices would be associated with the fact that the synodic motion of the Moon–the cycle of the phases from New Moon to Full Moon–is the difference between the sidereal motions of the Sun and of the Moon against the backdrop of the fixed stars. The Sun appears to rotate through the stars of the zodiac in about 365 days, while the Moon changes place in a period of about 27-1/3 days, and changes through its cycle of phases in about 29-1/2 days.
"Either the differential turntable adds the revolutions of the Sun to those of the synodic phenomena, to produce the revolutions of the Moon, or it subtracts the revolutions of the Sun from those of the Moon to produce the cycles of the synodic months. From the fact that B3 and B4 rotate in opposite directions (and so therefore do E1 and E2) it follows that it is the latter case which applies. This is confirmed by the gear ratios . . . which introduce numbers compatible with the classical Greek calendrical device of the Metonic cycle, in which 19 solar years are made to correspond exactly with 235 lunations, and therefore with 254 sidereal revolutions of the Moon. The gearing contains wheels that correspond very well with the prime numbers 19 and 127 which are needed to mechanize the Metonic cycle. We have in fact 64/383 48/243 127/32 = 254/19, so that the differential gear is fed with 254 revolutions of E2 and 19 reverse revolutions of E1. For every 19 (direct) turns of the main drive wheel; this produces 2,356/2 revolutions of the whole differential turntable and all the gears mounted upon it."
|
|
|
|
|
|