|
|
|
 |
|
|
|
Why You Don't Believe Fermat's Principle
Laurence Hecht
(Full text of editorial from Fall 2001 21st Century)
|
|
| Snell's Discovery
Fermat's Principle
Intention in Nature
The Political Issue of ‘Human Cloning'
|
|
Confusion over the meaning of the term universal physical principle may be more prevalent in science today than at any time in history. In former times, although great differences existed on this matter, they were usually discussed. Today, we don't even bother. Hence, the most contradictory views coexist within the body of knowledge mis-termed modern science.
One of the clearest dividing lines is over the matter of intention in nature. Despite the overwhelming evidence of a purposefulness in natural development, the modern view has replaced the idea of intention with that of mechanism. A theory is called scientific if it provides a credible mechanism, or model, to describe an observable natural phenomena.
In one such model, dead objects (often called particles) are assumed to exist and are assigned certain properties, such as attraction, repulsion, or inertia, which must be assumed as axiomatic. These objects exist in an empty, triply-extended container, called space, to which certain self-evident properties are attributed, while a fourth dimension, called time, extends linearly into the before and after. In another version, the space is not empty, but filled with a substance capable of transmitting waves, which replace the particles as the self-evident elementarity.
In modern times, we have added various complex variations to these mechanistic systems. In one, the ether disappears, but the waves, and particles, still exist. And there are others, but none that has challenged the essential premises of mechanism.
Wide acceptance of a fraudulent version of the history of science has allowed the flourishing of the modern prejudice that the method of mechanism has produced scientific discovery. (We can show that it has never led to scientific discovery, but only to its suppression.) We take the case of Fermat's Principle of Least Time to help the modern reader to understand that a true universal physical principle will be an expression of intention in the universe. A close examination of the criticism to which Fermat's Principle was subjected by the Cartesians, will help the reader to see the prejudices he likely brings to the subject.
Snell's Discovery
The law of reflection of light, that the angle of incidence equals the angle of reflection, was known in classical times. Heron of Alexandria recognized that this law obeyed a minimal principle; that is, that were the angles to differ from each other, the time and distance of travel of the light would not be the least possible.
The law governing the refraction of light proved more difficult to discover. When a ray of light passes from one medium to another, it is bent (refracted). If the passage is from a less dense to a more dense medium, the light bends toward the normal to the surface forming the boundary between the two media. However, the angle of refraction varies, in some non-linear way, with the angle of incidence. The problem of lawfully determining this angle had been under investigation since Classical times. Neither the great optical theorists of the Arab renaissance, nor those of Europe could solve it.
Finally, in 1621, Willebrord Snell, a leading mathematical physicist of the Dutch republican tradition, found the solution. The light ray is refracted in such a way that the sines of the angles of incidence and refraction remain in the same proportion for any given pair of media (see Figure 1).
|
|
|
|
|
|
 |
|
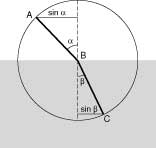
Figure 1
SNELL'S LAW OF SINES
When a light ray passes from a rarer to a denser medium, it is bent toward the normal (dotted line). The relationship between the angles a and b was not known, until Willebrord Snell discovered in 1621 that the sines of the angles maintain a constant proportion for any given pair of media.
|
|
|
|
|
|
|
Snell's discovery was welcomed by René Descartes (1596-1650), the leader of a philosophical school which proposed that all natural phenomena could be explained by mechanical causes. In fact, Descartes so welcomed the discovery that he claimed it for his own, and his writings being more widely read than Snell's, Descartes was thought to be the discoverer of the law, until the matter was cleared up after his death.
Descartes was not content, however, to express the law as Snell discovered it. It was necessary to fit it into his mechanistic philosophy of nature, in which he represented light as consisting of ballistic particles. In order to thus account for the law of refraction, Descartes had to make the unusual assumption that the particles speed up when they pass from a less dense to a more dense medium. This seemed absurd to many. However, as no one was able to accurately measure the velocity of light in its passage from one medium to another, this assumption was not finally disproven experimentally until the middle of the 19th Century, when Leon Foucault and Armand Fizeau designed an experimental apparatus which proved Descartes wrong.
Fermat's Principle
Pierre de Fermat (1601-1665) was one of those classically educated geniuses, who, like Ampère, never went to college. Having received an early education in Greek and Latin, Fermat read the mathematical classics of antiquity in the originals, and so developed his mind. (Ampère never even went to elementary school, but learned by reading in his father's library; he taught himself Latin at the age of 11, in order to be able to read Bernoulli's calculus.)
Fermat did not believe Descartes's assertion about the velocity of light. After a long and fruitless correspondence with the followers of Descartes, he came upon a new flank of attack. In 1657, in a letter to Cureau de la Chambre, Fermat stated for the first time his idea that the law of refraction might be deduced from a minimum principle, like that which Heron had noted for reflection.1
In a letter of Jan. 1, 1662, to Cureau de la Chambre, Fermat announced that he had accomplished his proof.2 Fermat showed that the path of a refracted ray of light was that which takes the least time! (See Figure 2.) The discovery, now known as Fermat's Principle of Least Time, was more than the Cartesians could stand. In fact, it is probably more than most readers can stand—they just don't know it.
|
|
|
|
|
|
 |
|
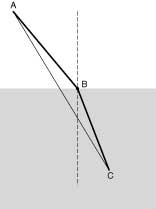
Figure 2
FERMAT'S PRINCIPLE OF LEAST TIME
In 1662, Pierre de Fermat proved that a ray of light passing from a rarer to a denser medium, follows the path which takes the least time. The straight line AC would not take the least time, because the ray, in this case, would be spending a larger part of its course moving more slowly in the denser medium.
|
|
|
|
|
|
|
|
To understand why you probably can't stand it, consider the following objections to Fermat's Principle made in May 1662 by Clerselier, an expert in optics and leading spokesman for the Cartesians on this matter3:
"1. The principle you take as a basis for your proof, to wit, that nature always acts by the shortest and simplest path, is only a moral principle, not a physical one—it is not and can not be the cause of any effect in nature."
Does anyone disagree? Clerselier continues:
"This principle is not the cause, because it is not the principle which makes the action, but rather the hidden force and power which reside in each thing, which things are never directed to a given effect by this principle, but rather by the force which results from all the causes that come together into a given action, and by the present disposition of all the bodies on which this force acts."
I argue that there is still nothing for the modern physicist to disagree with. If the phrase "hidden force and power which reside in each thing" sounds a bit strange, then what do you mean by a force of attraction, or by inertia?
Clerselier, again:
"And [Fermat's] principle can not be the cause, for otherwise we would be attributing knowledge to nature: and here, by nature, we understand only that order and lawfulness in the world, such as it is, which acts without foreknowledge, without choice, but by a necessary determination."
Don't we agree? Nature cannot act with foreknowledge. Is not evolution the result of random events, ordered by the survival of the fittest? Back to Clerselier:
"2. This same principle must make nature irresolute, not knowing which way to go when it makes a ray of light pass from a less dense to a more dense medium. For I ask you: if it is true that nature must always act by the shortest and simplest path, and given that the straight line is undoubtedly shorter and simpler than any other, would it not make nature hesitate, (if you wish that it act by this principle), when a ray of light, passing from a point in a rare medium to a point in a dense one, must simultaneously follow both the straight line and the bent one, since if the one proves shorter in time, the other is shorter and simpler in length? Who will decide, and who judge?"
Who indeed?
Intention in Nature
Finally, Clerselier argues:
"3. As it is not time which moves, it cannot be time which determines the motion, and when a body is once moved and set on a certain path, there is no reason to believe that time, greater or lesser, could cause this body to change its path, since time does not act on it and has no power over it. But, as the entire speed and direction of this body depend on its force and the disposition of its force, it is much more natural, and, in my view, much more scientific, to say as Mr. Descartes does, that the speed and direction of this body are altered by the alteration which takes place in the force and the disposition of this force, which are the true causes of its movement, and not to say as you do, that they change by an intention which nature possesses of always taking the path it can pursue most quickly, an intention which it cannot have, since it acts without knowledge, and thus has no effect on this body."
So, if we accept Clerselier's arguments, as almost every scientifically educated person today would have to admit he does, Fermat's Principle of Least Time is an absurdity. And yet it is true, and stands as one of the foundations of all our knowledge of nature. From it came the work of Leibniz and the Bernoullis on the cycloid and the non-algebraic curves, which were the heart of the development of the calculus. Fresnel's developments of the wave theory are based on it, and so everything we know of the electromagnetic spectrum, and so forth.
What then is wrong with your view of nature? We can hardly think of a better argument for the existence of intention in nature than that to which Clerselier leads us in his attempt to oppose it. We have been arguing for such a standpoint, the one which is the actual basis of all modern science, which begins with Nicholas of Cusa's great breakthrough in the De Docta Ignorantia (On Learned Ignorance), and proceeds through Leonardo, Kepler, and Leibniz, into the work of Gauss and Riemann, reaching unfortunately a temporary dead-end about that point.
But we have had some trouble getting your attention. Perhaps, if you have followed the argument, we can hope for a bit more success here.
Notes
1. Oeuvres de Fermat, Paris, 1891-1922, T. II, p. 354 (cited in C. Carathéodory, "The Beginning of Research in the Calculus of Variations," presented on Aug. 31, 1936 at the meeting of the Mathematical Association of America in Cambridge, Mass., during the tercentenary celebation of Harvard University).
2. Ibid, p. 457.
3. Ibid, p. 454.
|
|
|
|
|