Figure 1
THE FIVE PLATONIC SOLIDS
The five regular, or Platonic, solids are best conceptualized as the regular tilings of the surface of a sphere. They thus define a crucial boundary of what can be constructed in visual space. In nested arrangements, the solids and their implicit variations may represent a multiply connected manifold, which serves as a metaphor for the relationship of the individual to the whole universe in physical space. Construction of the solids, and exploration of their variations, has thus always been the foundation for creative work in science.
|
|
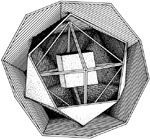 
Figure 2
A WORKING MODEL OF THE NUCLEUS
In the Moon model of the nucleus, a nesting of four of the five Platonic solids similar to that conceived by Johannes Kepler to describe the Solar System, is employed. Also shown is a photograph of a working model of the nucleus, made for Moon by retired machinist George Hamann in 1986. The scale model was constructed out of used aluminum offset printing plates. |
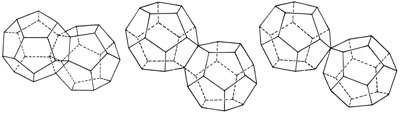
Figure 3
THE COMPLETED URANIUM NUCLEUS
(a) To go beyond palladium (atomic number 46), which is represented by the completed dodecahedron, an identifcal dodecahedron joins the first one at a face. When the second dodecahedron is completed, it is seen that six positions on the common dodecahedral face are already occupied. This represents the nucleus of radon (atomic number 86).
(b) To go beyond radon, the twin dodecahedra open up, using a common edge as if it were a hinge.
(c) To create 91-protactanium, the hinge is broken at one end. To create 92-uranium, the position where two protons join must be slightly displaced, creating the instability which permits fission. |
|
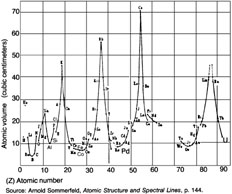
Figure 4
PERIODIC PROPERTIES OF THE ELEMENTS
The periodicity of the atomic volumes of the elements (the ratio of their atomic weight to density) guided Lothar Meyer in the 19th-century in developing the periodic table. The maxima in the graph at atomic numbers 3, 11, 19, 55, and 87 identify the Group 1A elements that begin each period. However, minima occur in the same graph at or near the atomic numbers 8, 14, 26, and 46, which mark the completed proton shells in the Moon nucleus. |
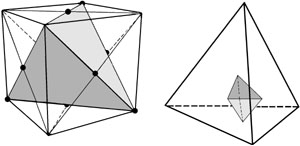
Figure 5
TETRAHEDRON INSCRIBED IN A CUBE
Every cube implies a tetrahedron. Four diagonally opposite vertices of the cube form the vertices of the tetrahedron (a). The alpha particle is conceived as a smaller tetrahedron (b), whose vertices fit at the centers of the faces of the larger tetrahedron pictured in (a).
|
|
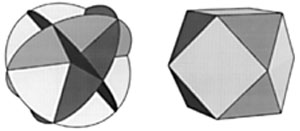
Figure 6
THE FOUR ‘CURRENT RING’ CONFIGURATION
Consider the four hoops pictured as four current-carrying loops. Their magnetic poles would point to the centers of the eight triangles formed by the intersection of the hoops. These correspond to the eight vertices of a cube. |
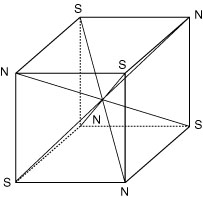
Figure 7
FORMATION OF DIPOLES
Dipoles formed by long diagonals on a cube create stability at each vertex.
|
|
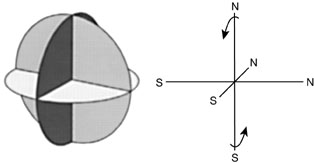
Figure 8
INSTABILITY OF OCTAHEDRAL MAGNETIC DIPOLES
Three circular loops (a) in which the poles point to the six vertices of the octahedron. The magnetic dipoles in this configuration (b) must be unstable; for example, the north pole at top experiences rotational moment. |
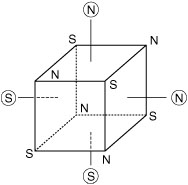
Figure 9
OCTAHEDRAL VERTICES INSIDE A CUBE
The octahedral vertices (circled) standing above the face centers of a cube, are stable with respect to the magnetic polarity of cube vertices.
|
|
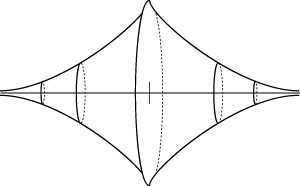
Figure 10
MAGNETIC STRENGTH AROUND A WEBER ‘MOLECULAR AGGREGATE’
The circles represent the magnetic strength around Weber’s “molecular aggregate” of two protons, and form a double, exponential, pseudosphere-like solid of rotation. |